Chapter 6 数理统计的基本概念¶

约 3852 个字 11 张图片预计阅读时间 19 分钟

随机样本与统计量¶

总体：研究对象的全体；
个体：总体中的成员；
总体的容量：总体中包含的个体数；
有限总体：容量有限的总体；
无限总体：容量无限的总体，通常将容量非常大的总体也按无限总体处理。

总体的某个指标 $X$ : 对于不同的个体来说有不同的取值, 这些取值可以构成一个分布, 因此 $X$ 可以看成一个随机变量。有时候就把 $X$ 称为总体。假设 $X$ 的分布函数为 $F(x)$ , 也称 $F(x)$ 为总体。
样本：从总体中抽取的个体组成的集合；
随机样本：从总体中随机地取 $n$ 个个体；
简单随机样本：满足以下两个条件的随机样本 $(X_1,X_2,\cdots,X_n)$ 称为容量是 $n$ 的简单随机样本：
1. 代表性：每个 $X_1$ 与 $X$ 同分布；
2. 独立性：$X_1,X_2,\cdots,X_n$ 是相互独立的随机变量。

Info

后面提到的样本均指简单随机样本。

(1)一个容量为 $n$ 的样本 $(X_1,X_2,\cdots,X_n)$ 是指 $n$ 个独立与总体分布相同的随机变量。

(2)一旦对样本进行观察，得到的实际数值 $(x_1,x_2,\cdots,x_n)$ 称为样本观察值(或样本值)。

(3)两次观察，样本值可能是不同的。

若总体 $X$ 具有概率密度 $f(x)$ , 则样本 $(X_1,X_2,\cdots,X_n)$ 具有联合概率密度函数： $f_n(x_1,x_2,\cdots,x_n) = \prod\limits_{i=1}^n f(x_i)$

关于上述联合概率密度函数

由于样本为简单随机样本，也即独立同分布。因此可以直接相乘得到联合概率密度函数。

统计量：¶

样本的不含任何未知参数的函数。

设 $(X_1,X_2,\dots,X_n)$ 为样本，若 $g(X_1,X_2,\dots,X_n)$ 不含任何未知参数，则称 $g(X_1,X_2,\dots,X_n)$ 为统计量。

常用统计量：

样本均值： $\overline{X} = \frac{1}{n}\sum\limits_{i=1}^n X_i$
样本方差： $S^2 = \frac{1}{n-1}\sum\limits_{i=1}^n (X_i - \overline{X})^2$
样本标准差： $S = \sqrt{S^2}$
样本 $k$ 阶矩： $A_k = \frac{1}{n}\sum\limits_{i=1}^n X_i^k$
样本 $k$ 阶中心矩： $B_k = \frac{1}{n}\sum\limits_{i=1}^n (X_i - \overline{X})^k\ ,k=1,2,\dots$

Question

设 $X$ 为总体，$X_1,X_2,\cdots,X_n$ 是样本， $E(X) = \mu$ 存在，则 $\overline{X} = \mu$ 对吗？

Answer

不对。

$E(X) = \mu$ 是一个数，可能已知，可能未知；

$\overline{X}$ 是随机变量，依赖于样本值，对于不同的样本值，$\overline{X}$ 的取值可能不一样。

Info

用样本均值估计总体均值，可能估计过高，也可能估计过低。所有样本均值的平均值恰好是总体均值。(无偏)
总体方差 $\sigma^2$ 的估计可以用 $S^2$ ，也可以用 $B_2$ 。但当 $\sigma^2 > 0$ 时，$E(S^2) = \sigma^2,E(B_2) \neq \sigma^2$ 所以 $S^2$ 是无偏的， $B_2$ 是有偏的。

三大分布¶

$\chi^2$-分布/卡方分布¶

设随机变量 $X_1,\dots,X_n$ 相互独立，且都服从标准正态分布 $N(0,1)$ ，则称随机变量 $\chi^2 = \sum\limits_{i=1}^n X_i^2$ (1)

服从自由度为 $n$ 的 $\chi^2$-分布，记为 $\chi^2 \sim \chi^2(n)$ 。

自由度指(1)式右端包含的独立变量的个数。

$\chi^2$-分布的概率密度函数为(不要求)：

\[f(x) = \begin{cases} \frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}} & x > 0 \\ 0 & x \leq 0 \end{cases} \ ,n > 0\]

其中 $\Gamma(\alpha) = \int_0^{+\infty} x^{\alpha-1}e^{-x}dx$ 。

$\chi^2$-分布的性质¶

设 $\chi^2 \sim \chi^2(n)$ ，则 $E(\chi^2) = n$ ， $D(\chi^2) = 2n$ 。

证明

(1)

\[E(X_i^2) = D(X_i) + E^2(X_i) = 1\]

\[E(\chi^2) = E(\sum\limits_{i=1}^n X_i^2) = \sum\limits_{i=1}^n E(X_i^2) = n\]

(2)

\[D(\chi_i^2) = E(\chi_i^4) - E^2(\chi_i^2)\]

\[E(\chi_i^4) = \int_0^{+\infty} x^4 \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx = 3\]

\[\therefore D(\chi_i^2) = 2\]

\[\therefore D(\chi^2) = 2n\]

$\chi^2$分布的可加性：

设 $Y_1 \sim \chi^2(n_1)$ ， $Y_2 \sim \chi^2(n_2)$ ，且 $Y_1$ ， $Y_2$ 相互独立，则 $Y_1 + Y_2 \sim \chi^2(n_1 + n_2)$ 。

设 $Y_1,\dots,Y_m$ 相互独立，且 $Y_i \sim \chi^2(n_i)$ ，则 $\sum\limits_{i=1}^m Y_i \sim \chi^2(\sum\limits_{i=1}^m n_i)$ 。
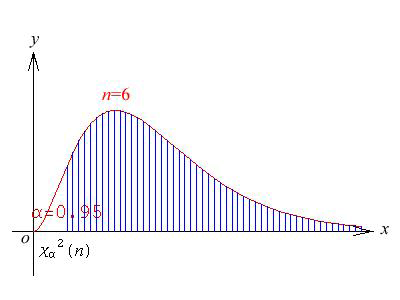
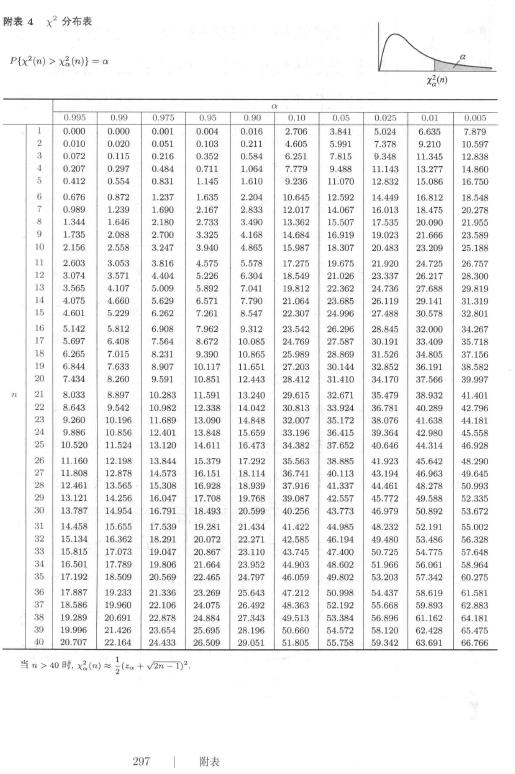
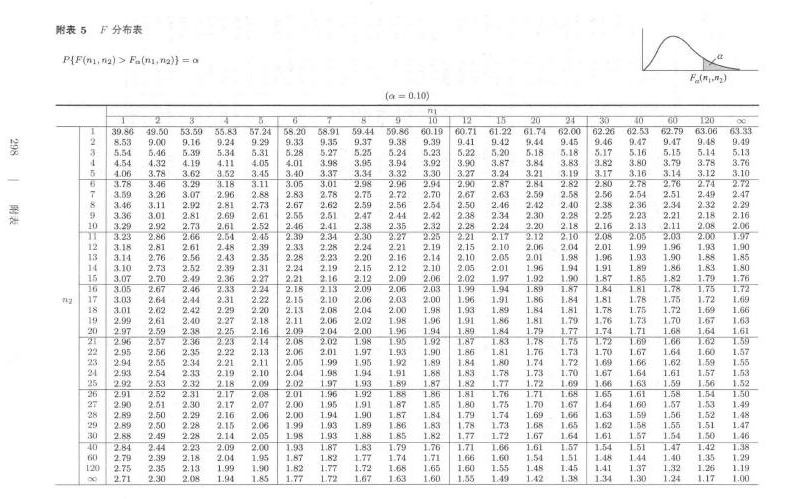
$\chi^2_\alpha(n)$ 为 $\chi^2(n)$分布的上 $\alpha$ 分位数，即给定 $\alpha$ , $0<\alpha<1$ ,满足 $P(\chi^2 > \chi^2_\alpha(n)) = \alpha$ 。

$\chi^2$ 分布的概率密度函数

$\chi^2$ 分布的上 $\alpha$ 分位数

$\chi^2$ 分布的上 $\alpha$ 分位数表

Question

设总体 $X \sim N(\mu,\sigma^2)$ ， $\mu , \sigma^2$ 已知。 $X_1,\dots,X_n$ 是来自总体 $X$ 的样本，求统计量 $\chi^2 = \frac{1}{\sigma^2}\sum\limits_{i=1}^n (X_i - \mu)^2$ 的分布。

Answer

作变换 $Y_i = \frac{X_i - \mu}{\sigma}$ ，则 $Y_i \sim N(0,1)$ ，且 $Y_1,\dots,Y_n$ 相互独立，则 $\chi^2 = \sum\limits_{i=1}^n Y_i^2 \sim \chi^2(n)$ 。

$t$-分布/学生氏分布¶

设 $X \sim N(0,1)$ ， $Y \sim \chi^2(n)$ ，且 $X$ ， $Y$ 相互独立，则称随机变量

\[T = \frac{X}{\sqrt{\frac{Y}{n}}}\]

服从自由度为 $n$ 的 $t$-分布，记为 $T \sim t(n)$ 。

$t$-分布的概率密度函数为(不要求)：

\[f(t,n) = \frac{\Gamma(\frac{n+1}{2})}{\sqrt{n\pi} \cdot \Gamma(\frac{n}{2})}(1+\frac{t^2}{n})^{-\frac{n+1}{2}} \ ,-\infty < t < +\infty\]

其中， $\Gamma(\alpha) = \int_0^{+\infty} x^{\alpha-1}e^{-x}dx$ 。$\Gamma(\alpha +1) = \alpha \Gamma(\alpha) = \alpha !(if \alpha \in Z), \Gamma(0.5) = \sqrt{\pi}$

$t(n)$ 分布概率密度函数

$t$ 分布的上 $\alpha$ 分位数

$t$ 分布的上 $\alpha$ 分位数表

$t$-分布的性质¶

设 $T \sim t(n)$ 当 $n \ge 2$ 时， $E(T) = 0$ ， $D(T) = \frac{n}{n-2}$ ， $n > 2$ 。

证明

\[E(T) = \int_{-\infty}^{+\infty} t \cdot f_T(t)dt\]

由于 $t \cdot f_T(t)$ 在 $-\infty$ 到 $+\infty$ 上是奇函数，所以 $E(T) = 0$ 。

\[D(T) = E(T^2) - [E(T)]^2\]

\[E(T^2) = \int_{-\infty}^{+\infty} t^2 \cdot f_T(t)dt = \int_{-\infty}^{+\infty} \frac{\Gamma(\frac{n+1}{2})}{\sqrt{n\pi}\Gamma(\frac{n}{2})}(1+\frac{t^2}{n})^{-\frac{n+1}{2}} \cdot t^2dt\]

通过特殊积分公式计算得到 $D(T) = E(T^2) = \frac{n}{n-2} \ for \ n>2$ 。

ATTENTION

不能直接通过 $\frac{E(X)}{E(Y)}$ 来计算 $E(T)$ , 这是因为 $T$ 是由 $X$ 和 $Y$ 的比值定义的随机变量，而 $X$ 与 $Y$ 是非线性变换的。

换句话说，能够直接相除的情况非常有限，需要满足下述条件：

(1) $X$ 和 $Y$ 相互独立；

(2) $Y$ 始终非零；

(3) $X$ 和 $Y$ 的分布足够简单，例如 $X$ 和 $Y$ 都是常数或线性相关( e.g. $Y=aX$ )的情况。

当 $n \to +\infty$ (或 $n \ge 45$ 时可认为)， $t(n) \to N(0,1)$ 。

证明

运用中心极限定理。

由于 $E(Y) = n, D(Y) = 2n$ 可以得到 $\sqrt{\frac{Y}{n}} \xrightarrow{P} 1 \quad \text{当 } n \to \infty$ 。

对于任意固定的 $Z \sim N(0,1)$，有：

\[T_n = \frac{Z}{\sqrt{Y/n}} \to Z \quad \text{当 } n \to \infty\]

设 $T \sim t(n)$ ， $N \sim N(0,1)$ ，则对于任意的 $n \ge 1$ , 都存在 $a_0 > 0$ ，使得 $P(|T| \ge a_0) \ge P(|N| \ge a_0)$ 。
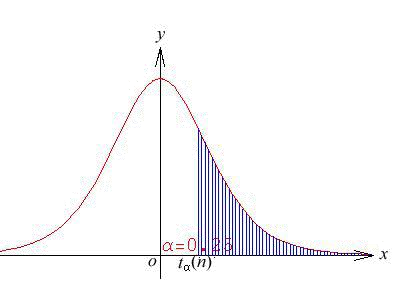
$t_{\alpha}(n)$ 为 $t(n)$ 分布的上 $\alpha$ 分位数，即给定 $\alpha$ , $0<\alpha<1$ ,满足条件 $\int_{t_{\alpha}(n)}^{+\infty}f(t,n)dt = \alpha$ 。
$t_{1-\alpha}(n) = -t_{\alpha}(n)$ 。

证明

\[\forall 0<\alpha < 1, P(T > t_{\alpha}(n)) = \alpha\]

\[P(T < t_{\alpha}(n)) = 1 - \alpha\]

由于 $t$ 分布的对称性可得:

\[P(T < -t_{\alpha}(n)) = \alpha\]

\[\because P(T > t_{1- \alpha}(n)) = 1 - \alpha\]

\[\therefore P(T < t_{1- \alpha}(n)) = \alpha\]

\[\therefore t_{1-\alpha}(n) = -t_{\alpha}(n)\]

$F$-分布¶

设 $X \sim \chi^2(n_1)$ ， $Y \sim \chi^2(n_2)$ ，且 $X$ ， $Y$ 相互独立，则称随机变量

\[F = \frac{\frac{X}{n_1}}{\frac{Y}{n_2}}\]

服从自由度为 $(n_1,n_2)$ 的 $F$分布，记为 $F \sim F(n_1,n_2)$ 。

其中 $n_1$ 称为第一自由度， $n_2$ 称为第二自由度。

$F(n_1,n_2)$分布的概率密度函数为(不要求)：

\[f(x,n_1,n_2) = \begin{cases} \frac{1}{B(\frac{n_1}{2},\frac{n_2}{2})}n_1^{\frac{n_1}{2}}n_2^{\frac{n_2}{2}}x^{\frac{n_1}{2}-1}(n_2+n_1x)^{-\frac{n_1+n_2}{2}} & x > 0 \\ 0 & x \le 0 \end{cases}\]

其中， $B(\alpha,\beta) = \int_0^1 x^{\alpha-1}(1-x)^{\beta-1}dx = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$ 。

$F$ 分布的概率密度函数

$F$ 分布的上 $\alpha$ 分位数

$F$ 分布的上 $\alpha$ 分位数表

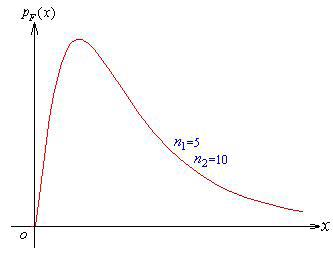
关于 $F$ 分布的图像

F分布的概率密度函数（PDF）依赖于两个自由度参数，分别记作 $n_1$ 和 $n_2$ ，也称为分子自由度和分母自由度。

随着 $n_1$ 增加：
- 当 $n_1$ 增大时，F分布的峰值会向右移动，并且分布变得更加集中。也就是说，随着 $n_1$ 的增大，分布的偏斜性减小，图形变得更对称。
- 对于非常大的 $n_1$ ，F分布趋近于一个正态分布。
随着 $n_2$ 增加：
- 当 $n_2$ 增大时，F分布的右尾变轻，即极端值出现的概率减少，分布更加集中在均值附近。
- 类似地，当 $n_2$ 变得非常大时，F分布也会趋近于一个正态分布。
对于较小的 $n_1$ 和 $n_2$ ：
- F分布通常会有较长的右尾，表示较大的方差，分布更分散，具有较高的偏斜性。
- 分布的峰值较低，因为概率质量分布在较宽的范围内。
总体趋势：
- 总体来说，随着 $n_1$ 和 $n_2$ 都增加，F分布趋向于更紧凑、更对称，并且其形态逐渐接近正态分布。
- 两个自由度都为1的情况下，F分布等价于柯西分布，它有一个特别长的尾部并且没有定义的平均值或方差。

$F$-分布的性质¶

设 $F \sim F(n_1,n_2)$ ,则 $F^{-1} \sim F(n_2,n_1)$ 。
设 $X \sim t(n)$ ，则 $X^2 \sim F(1,n)$ 。
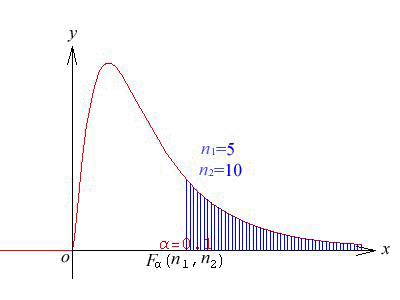
$F_{\alpha}(n_1,n_2)$ 为 $F(n_1,n_2)$ 的上 $\alpha$ 分位数，即给定 $\alpha$ , $0<\alpha<1$ ,满足条件 $\int_{F_{\alpha}(n_1,n_2)}^{\infty}f(x,n_1,n_2)dx = \alpha$ 。
$F_{1-\alpha}(n_1,n_2) = \frac{1}{F_{\alpha}(n_2,n_1)}$ 。

证明

\[F \sim F(n_1,n_2) \Rightarrow F^{-1} \sim F(n_2,n_1)\]

\[\alpha = P(F \ge F_{\alpha}(n_1,n_2)) = P(F^{-1} \le F_{\alpha}^{-1}(n_1,n_2)) = 1 - P(F^{-1} > F_{\alpha}^{-1}(n_1,n_2))\]

\[\Rightarrow P(F^{-1} > F_{\alpha}^{-1}(n_1,n_2)) = 1 - \alpha\]

\[\because F^{-1} \sim F(n_2,n_1)\]

\[\therefore F_{1-\alpha}(n_2,n_1) = \frac{1}{F_{\alpha}(n_1,n_2)}\]

\[\therefore F_{1-\alpha}(n_1,n_2) = \frac{1}{F_{\alpha}(n_2,n_1)}\]

Question

$X,Y,Z$ 相互独立，均服从 $N(0,1)$ ，则

(1) $X^2+Y^2+Z^2$ 的分布是什么？

(2) $\frac{X}{\sqrt{Y^2+Z^2}}$ 的分布是什么？

(3) $\frac{2X^2}{Y^2+Z^2}$ 的分布是什么？

Answer

(1) $X^2+Y^2+Z^2 \sim \chi^2(3)$ 。

(2) $\frac{X}{\frac{\sqrt{Y^2+Z^2}}{2}} \sim t(2)$ 。

(3) $\frac{2X^2}{Y^2+Z^2} \sim F(1,2)$ 。

单个正态总体的抽样分布¶

定理一¶

设总体 $X \sim N(\mu,\sigma^2)$ ， $X_1,X_2,\cdots,X_n$ 是样本，样本均值 $\overline{X} = \frac{1}{n}\sum\limits_{i=1}^nX_i$ , 样本方差 $S^2 = \frac{1}{n-1}\sum\limits_{i=1}^n(X_i-\overline{X})^2$ ，则

\[\overline{X} \sim N(\mu,\frac{\sigma^2}{n})\]

\[\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0,1)\]
$\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)$ 且 $\overline{X}$ 与 $S^2$ 相互独立。

直观理解

这里就涉及到对自由度的理解了。让我们先看看对自由度的定义。

自由度：是指当以样本的统计量来估计总体的参数时，样本中独立或能自由变化的数据的个数，称为该统计量的自由度。一般来说，自由度等于独立变量减掉其衍生量数。也能理解为自由度是一个随机向量的维度数，也就是一个向量能被完整描述所需的最少单位向量数。

在这里，对于 $\sum\limits_{i=1}^n(X_i-\overline{X})$ ，可以看到 $n-1$ 个维度即可描述。

可以想见，样本方差 $S^2$ 只依赖于样本数据的偏差部分，即 $(X_1-\overline{X}),(X_2-\overline{X}),\cdots,(X_n-\overline{X})$ ，而与 $\overline{X}$ 无关。所以 $\overline{X}$ 与 $S^2$ 相互独立。

此时我们就可以得到上述两条定理了。

此处附上老师给的证明

Question

设总体 $X \sim N(\mu,\sigma^2)$ , $X_1,X_2,\cdots,X_n$ 是样本。

(1) $\frac{\sum\limits_{i=1}^n(X_i-\overline{X})^2}{\sigma^2}$ 服从什么分布？

(2) $\frac{\sum\limits_{i=1}^n(\overline{X}-\mu)^2}{\sigma^2}$ 服从什么分布？

Answer

(1) $\chi^2(n-1)$

(2) $\chi^2(n)$

定理二¶

设总体 $X \sim N(\mu,\sigma^2)$ ， $X_1,X_2,\cdots,X_n$ 是样本，样本均值 $\overline{X} = \frac{1}{n}\sum\limits_{i=1}^nX_i$ , 样本方差 $S^2 = \frac{1}{n-1}\sum\limits_{i=1}^n(X_i-\overline{X})^2$ ，则

\[\frac{\overline{X} - \mu}{\frac{S}{\sqrt{n}}} \sim t(n-1)\]

证明

\[\frac{\overline{X} - \mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0,1)\]

\[\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)\]

\[\frac{\overline{X} - \mu}{\frac{S}{\sqrt{n}}} = \frac{\frac{\overline{X} - \mu}{\frac{\sigma}{\sqrt{n}}}}{\sqrt{\frac{(n-1)S^2}{\sigma^2}/(n-1)}} \sim t(n-1)\]

Question

设总体 $X$ 的均值 $\mu$ , 方差 $\sigma^2$ 存在。 $(X_1,\dots,X_n)$ 是取自总体 $X$ 的样本， $\overline{X}$ 是样本均值， $S^2$ 是样本方差。

(1) 求 $E(S^2)$

(2) 若 $X \sim N(\mu,\sigma^2)$ ，求 $D(S^2)$ .

Answer

\[\sum\limits_{i=1}^n(X_i-\overline{X})^2 = \sum\limits_{i=1}^n(X_i^2-2X_i\overline{X}+\overline{X}^2) = \sum\limits_{i=1}^nX_i^2 - n\overline{X}^2\]

\[E(S^2) = E[\frac{1}{n-1}\sum\limits_{i=1}^n(X_i-\overline{X})^2] = \frac{1}{n-1}[\sum\limits_{i=1}^nE(X_i^2) - nE(\overline{X}^2)]\]

\[= \frac{1}{n-1}[\sum\limits_{i=1}^n(\mu^2+\sigma^2) - n(\mu^2+\frac{\sigma^2}{n})] = \sigma^2\]

\[\text{无偏！}\]

由于 $\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)$

\[D[\frac{(n-1)S^2}{\sigma^2}] = 2(n-1)\]

\[D(S^2) = \frac{2\sigma^4}{(n-1)}\]

两个正态总体的抽样分布¶

设样本 $(X_1,\dots,X_{n_1})$ 来自总体 $X \sim N(\mu_1,\sigma_1^2)$ ，样本 $(Y_1,\dots,Y_{n_2})$ 来自总体 $Y \sim N(\mu_2,\sigma_2^2)$ ，且两个样本相互独立。样本均值分别为 $\overline{X}$ , $\overline{Y}$ ，样本方差分别为 $S_1^2$ , $S_2^2$ 。

抽样分布一¶

\[F = \frac{\frac{S_1^2}{\sigma_1^2}}{\frac{S_2^2}{\sigma_2^2}} = \frac{\frac{S_1^2}{S_2^2}}{\frac{\sigma_1^2}{\sigma_2^2}} \sim F(n_1-1,n_2-1)\]

证明

\[\frac{S_1^2}{\sigma_1^2} \sim \chi^2(n_1-1)\]

\[\frac{S_2^2}{\sigma_2^2} \sim \chi^2(n_2-1)\]

\[F = \frac{\frac{S_1^2}{\sigma_1^2}}{\frac{S_2^2}{\sigma_2^2}} = \frac{\frac{\chi_1^2}{n_1-1}}{\frac{\chi_2^2}{n_2-1}} \sim F(n_1-1,n_2-1)\]

抽样分布二¶

\[\frac{\overline{X} - \overline{Y} - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}} \sim N(0,1)\]

证明

\[\overline{X} - \overline{Y} \sim N(\mu_1 - \mu_2,\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2})\]

\[\frac{\overline{X} - \overline{Y} - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}} \sim N(0,1)\]

抽样分布三¶

当 $\sigma_1^2 = \sigma_2^2 = \sigma^2$ 时，

\[\frac{(\overline{X} - \overline{Y} - (\mu_1 - \mu_2))}{S_w\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim t(n_1 + n_2 - 2)\]

其中， $S_w^2 = \frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{n_1 + n_2 - 2}$ , $S_w = \sqrt{S_w^2}$ ($S_w$ 是联合样本方差)

证明

\[\frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{\sigma^2} \sim \chi^2(n_1 + n_2 - 2)\]

\[\frac{(\overline{X} - \overline{Y} - (\mu_1 - \mu_2))}{\sigma \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} / \sqrt{\frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{\sigma^2 (n_1 + n_2 -2)}} \sim t(n_1 + n_2 - 2)\]

Thinking

若 $\sigma^2$ 未知，为什么用 $S_w$ 来估计 $\sigma^2$ 而不是用 $S_1^2$ 或 $S_2^2$ 来估计 $\sigma^2$ ？

解答

$E(S_1^2) = \sigma^2$ , $E(S_2^2) = \sigma^2$ , $E(S_w^2) = \sigma^2$ 都是无偏的。

$D(S_1^2) = \frac{2\sigma^4}{n_1-1}$ , $D(S_2^2) = \frac{2\sigma^4}{n_2-1}$ , $D(S_w^2) = \frac{2\sigma^4}{n_1 + n_2 - 2}$

$D(S_w^2) < D(S_1^2) , D(S_2^2)$ 从直观来看， $S_w$ 比 $S_1$ 和 $S_2$ 包含更多 $\sigma^2$ 的信息。

Question

设总体 $X \sim N(\mu, \sigma^2)$ ， $X_1, X_2, \cdots, X_5$ 是来取自 $X$ 的样本，设 $a,b$ 是都不为零的数。

若 $a(X_1-X_2)^2 + b(2X_3 - X_4 - X_5)^2 \sim \chi^2(k)$ , 则 $a,b,k$ 各为多少？

Answer

\[\frac{X_1 - X_2}{\sqrt{2}\sigma} \sim N(0,1)\]

\[\frac{2X_3 - X_4 - X_5}{\sqrt{6}\sigma} \sim N(0,1)\]

\[\therefore a = \frac{1}{2\sigma^2} , b = \frac{1}{6\sigma^2} , k = 2\]

ATTENTION

关于上面这道题有一个需要注意的点。其实直观上也可以感觉得到， $2X_3$ 和 $X_3 + X_3$ 是不一样的，前者的方差会比后者要大。

Question

设总体 $X \sim N(\mu, \sigma^2)$ ， $X_1, X_2, \cdots, X_4$ 与 $Y_1, Y_2, \cdots, Y_9$ 是取自总体 $X$ 的两个独立样本， $\overline{X},S_1^2$ 和 $\overline{Y},S_2^2$ 分别是这两个样本的样本均值和样本方差。

求(1)若 $a\frac{\overline{X} - \overline{Y}}{S_1} \sim t(k)$ , 则 $a,k$ 分别为多少？

(2) $\frac{\sum\limits_{i=1}^4 (X_i - \mu)^2}{4S_2^2}$ 服从什么分布？

Answer

(1)

\[\overline{X} - \overline{Y} \sim N(0,\frac{13\sigma^2}{36})\]

\[\frac{\overline{X} - \overline{Y}}{\sqrt{\frac{13\sigma^2}{36}}} \sim N(0,1)\]

\[\frac{3S_1^2}{\sigma^2} \sim \chi^2(3)\]

\[\text{且} \overline{X} - \overline{Y} \text{与} S_1^2 \text{相互独立}\]

\[\therefore a = \pm \frac{1}{\sqrt{\frac{13\sigma^2}{36}}} , k = 3\]

(2)

\[\frac{1}{\sigma^2}\sum\limits_{i=1}^4 (X_i - \mu)^2 \sim \chi^2(4)\]

\[\frac{8S_2^2}{\sigma^2} \sim \chi^2(8)\]

\[\text{由} F \text{分布的定义知}\]

\[\frac{\sum\limits_{i=1}^4 (X_i - \mu)^2}{4S_2^2} \sim F(4,8)\]

Chapter 6 数理统计的基本概念¶

随机样本与统计量¶

统计量：¶

三大分布¶

\(\chi^2\)-分布/卡方分布¶

\(\chi^2\)-分布的性质¶

\(t\)-分布/学生氏分布¶

\(t\)-分布的性质¶

\(F\)-分布¶

\(F\)-分布的性质¶

单个正态总体的抽样分布¶

定理一¶

定理二¶

两个正态总体的抽样分布¶

抽样分布一¶

抽样分布二¶

抽样分布三¶

评论