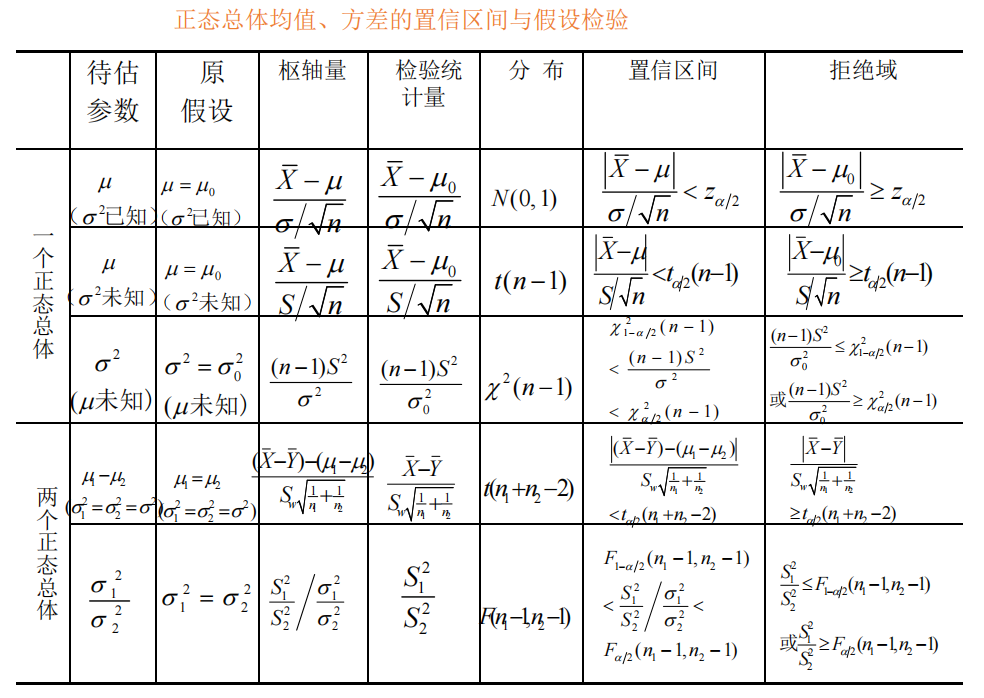
Chapter 8 假设检验¶
约 3701 个字 1 张图片 预计阅读时间 19 分钟
统计推断的另一类重要问题是假设检验问题。它包括
-
[参数检验] 已知总体分布的形式,需对其中的未知参数给出假设检验
-
[非参数检验]总体的分布形式完全未知的情况下,对总体的分布或数字特征进行假设检验
假设¶
原假设(零假设) \(H_0\) , 备择假设(对立假设) \(H_1\) 关于总体参数 \(\theta\) 的假设:
检验统计量和拒绝域¶
如果统计量 \(T = T(X_1, \cdots, X_n)\) 的取值大小和原假设 \(H_0\) 是否成立有密切练习,可将之称为对应假设问题的 检验统计量。
对应于拒绝原假设 \(H_0\) 时,样本值的范围成为 拒绝域, 记为 \(W\) , 其补集 \(\overline{W}\) 称为 接受域。
两类错误¶
由于样本的随机性,任一检验规则在应用时,都有可能发生错误的判断。
| 原假设为真 | 原假设为假 | |
|---|---|---|
| 根据样本拒绝原假设 | 第一类错误 | 正确决策 |
| 根据样本接受原假设 | 正确决策 | 第二类错误 |
-
第一类错误: 拒绝真实的原假设(弃真)
-
第二类错误: 接受错误的原假设(取伪)
犯第一类错误的概率
犯第二类错误的概率
例如 设某种清漆的9个样品,其干燥时间(以小时计)分别为: 6.0 5.7 5.5 6.5 7.0 5.8 5.2 6.1 5.0 根据以往经验,干燥时间的总体服从正态分布 N(6.0, 0.36), 现根据样本检验均值是否与以往有显著差异? (样本均值为6.4)
- 此时犯第一类错误的概率
\(\alpha(C) = P\{\text{拒绝} H_0 | H_0 \text{为真}\} = P\{|\overline{X}-6.0| \ge C | \mu = 6.0\}\)
\(= P\{\frac{|\overline{X}-6.0|}{\sqrt{\frac{\sigma^2}{n}}} \ge \frac{C}{\sqrt{\frac{\sigma^2}{n}}} | \mu = 6.0\}\)
由于当 \(H_0\) 成立时,即 \(\mu = 6.0\) , \(\frac{\overline{X}-6.0}{\sqrt{\frac{\sigma^2}{n}}} \sim N(0, 1)\) , 所以
\(\alpha(C) = 2 - 2\Phi(\frac{C}{\sqrt{\frac{\sigma^2}{n}}})\)
关于 C 是单调减函数
- 此时犯第二类错误的概率
\(\beta(C) = P\{\text{接受} H_0 | H_0 \text{为假}\} = P\{|\overline{X}-6.0| < C | \mu \ne 6.0\}\)
\(= P\{\frac{6.0-C-\mu}{\sqrt{\frac{\sigma^2}{n}}} \le \frac{\overline{X}-\mu}{\sqrt{\frac{\sigma^2}{n}}} \le \frac{6.0+C-\mu}{\sqrt{\frac{\sigma^2}{n}}} | \mu \ne 6.0\}\)
\(= \Phi\{\frac{6.0+C-\mu}{\sqrt{\frac{\sigma^2}{n}}}\} - \Phi\{\frac{6.0-C-\mu}{\sqrt{\frac{\sigma^2}{n}}}\},\mu \ne 6.0\)
关于 C 是单调增函数
所以,犯两类错误的概率相互制约!
Neyman-Pearson 原则¶
首先控制犯第一类错误的概率不超过某个常数 \(\alpha \in (0,1)\) ,再寻找检验,使得犯第二类错误的概率尽可能小。
其中的常数 \(\alpha\) 称为显著水平。
常取 \(\alpha = 0.01,0.05,0.10\) 等。
继续上面的例题
当 \(H_0\) 成立时:
若取 \(\alpha = 0.05\) ,则拒绝域为 \(\{|\overline{X} - 6| \ge 0.392|\}\)
\(\because \overline{x} = 6.4,|\overline{x}-6|=0.4 > 0.392\)
即 \(\overline{x}\) 落在拒绝域内, \(\overline{x}\) 与 \(\mu = 6\) 的差异显著,因此拒绝原假设,认为干燥时间的均值与以往有显著差异。
犯第1类错误的概率 \(\alpha(0.392)=0.05\)
犯第2类错误的概率 \(\beta(0.392) = P\{\text{接受}H_0|H_0\text{是假的}\} = P\{|\overline{X}-6.0|<0.392 | \mu \neq 6.0\}\)
\(= P\{5.608 < \overline{X} < 6.392| \mu \neq 6.0\} = \Phi\{\frac{6.392-\mu}{0.2}\} - \Phi\{\frac{5.608-\mu}{0.2}\},\mu \neq 6.0\)
例当 \(\mu = 5.4\) 时,
\(\beta = \Phi\{\frac{6.392-5.4}{0.2}\} - \Phi\{\frac{5.608-5.4}{0.2}\} \approx 0.15\)
P_ 值与统计显著性¶
P_ 值: 当原假设成立时,检验统计量取比观察到的结果更为极端的数值的概率.
例1中P_ 值的计算
P_ = \(P_{H_0}(|\overline{X}-6.0| \ge 0.4) = P_{H_0}(|\frac{\overline{X}-6.0}{0.2}| \ge 2) = 2 - 2\Phi(2) = 0.046 < 0.05\)
\(|\overline{X}-6.0| > 0.4\) 是小概率事件.作出拒绝原假设的判断.
P_ 值与显著水平 \(\alpha\) 的关系:
若 P_ \(\le \alpha\) ,则拒绝原假设,此时称检验结果在水平 \(\alpha\) 下是统计显著的.
若 P_ \(> \alpha\) ,则接受原假设,此时称检验结果在水平 \(\alpha\) 下是统计不显著.
处理假设检验问题的基本步骤¶
(1) 根据实际问题提出原假设和备择假设;
(2) 提出检验统计量和拒绝域的形式;
(3) 在给定的显著水平 \(\alpha\) 下,根据 Neyman-Pearson 原则求出拒绝域的临界值。
(4) 根据实际样本观测值作出判断。
(3') 计算检验统计量的观测值与 P_ 值;
(4') 根据给定的显著水平 \(\alpha\) ,作出判断.
[注:] \(H_0\) 与 \(H_1\) 地位不等
由于控制犯第1类错误,因此错误拒绝 \(H_0\) 是小概率事件,也就是说 \(H_0\) 不会轻易被拒绝掉。因此如果落在拒绝域,则说明已有了显著的差异,从而拒绝 \(H_0\)
\(H_0\) 选取: 不能轻易拒绝的,后果严重的,或维持现状的
如: \(H_0\) : 新技术未提高效益 \(\leftrightarrow H_1\) : 新技术提高效益
单个正态总体参数的假设检验¶
设样本 \(X_1,X_2,\dots,X_n\) 来自正态总体 \(N(\mu,\sigma^2)\) , \(\overline{X}\) 和 \(S^2\) 分别为样本均值和方差,显著性水平为 \(\alpha\)
有关均值 \(\mu\) 的检验
\(\sigma^2\) 已知时——Z检验
双边假设问题 \(H_0 : \mu = \mu_0,H_1 : \mu \neq \mu_0\)
取检验统计量为 \(Z = \frac{\overline{X} - \mu_0}{\sigma / \sqrt{n}}\)
在 \(H_0\) 为真时, \(Z \sim N(0,1)\)
根据 Neyman-Pearson 原则,检验的拒绝域为 \(W = \{|z| = |\frac{\overline{x}-\mu_0}{\sigma / \sqrt{n}}| \ge z_{\alpha / 2}\}\)
P_ 值的计算 对给定的样本观察值 \(x_1,\dots,x_n\) ,记检验统计量 Z 的取值为 \(z_0 = \frac{\overline{x} - \mu_0}{\sigma / \sqrt{n}}\) 则有
P_ \(= P_{H_0} \{ |Z| \ge |z_0| \} = 2(1 - \Phi (|z_0|))\)
当 P_ 小于显著水平 \(\alpha\) 时,拒绝原假设,否则,接受原假设.
右边检验 \(H_0 : \mu \le \mu_0,H_1 : \mu > \mu_0\)
检验统计量为 \(\overline{X}\) , 检验拒绝域的形式为 \(\overline{X} - \mu_0 \ge k\)
当 \(\mu \in H_0\) ,即 \(\mu \le \mu_0\) 时
\(\because \overline{X} \sim N(\mu,\frac{\sigma^2}{n})\)
\(\therefore \text{犯第一类错误概率为} P_{\mu}\{\overline{X} - \mu_0 \ge k\} = 1 - \Phi(\frac{k+\mu_0 - \mu}{\sigma / \sqrt{n}}) = \Phi(\frac{\mu - \mu_0 - k}{\sigma / \sqrt{n}}) \text{是} \mu \text{的增函数}\)
\(\therefore \text{当} \mu = \mu_0 \text{时,犯第一类错误概率最大.}\)
故只要 \(\Phi(\frac{-k}{\sigma / \sqrt{n}}) = \alpha\) ,即 \(\frac{-k}{\sigma / \sqrt{n}} = -z_{\alpha}\) 便可
因此,拒绝域为: \(\{z = \frac{\overline{x} - \mu_0}{\sigma / \sqrt{n}} \ge z_{\alpha} \}\)
P_ 值的计算 P_ = \(\mathop{sup}\limits_{\mu \le \mu_0} P_{H_0} \{Z \ge z_0 \} = P\{Z \ge z_0 | \mu = \mu_0 \} = 1 - \Phi (z_0)\)
结论¶
1 \(\sigma^2\) 已知检验 \(\mu\) (Z 检验法)¶
\(z_0 = \frac{\overline{x} - \mu_0}{\sigma / \sqrt{n}}\) ,当 \(\mu = \mu_0\) 时, \(Z = \frac{\overline{X} - \mu_0}{\sigma / \sqrt{n}} \sim N(0,1)\)
(1) \(H_0 : \mu = \mu_0 \leftrightarrow H_1 : \mu \ne \mu_0\)
拒绝域 : \(|Z| \ge z_{\alpha / 2}\)
P_ = \(P_{\mu_0} \{|Z| \ge |z_0| \} = 2(1 - \Phi(|z_0|))\)
(2) \(H_0 : \mu \le \mu_0 \leftrightarrow H_1 : \mu > \mu_0\)
拒绝域 : \(Z \ge z_{\alpha}\)
P_ = \(P_{\mu_0} \{Z \ge z_0 \} = 1 - \Phi(z_0)\)
(3) \(H_0 : \mu \ge \mu_0 , H_1 : \mu < \mu_0\)
拒绝域 : \(Z \le -z_{\alpha}\)
P_ = \(P_{\mu_0} \{Z \le z_0 \} = \Phi(z_0)\)
2 \(\sigma^2\) 未知检验 \(\mu\) (t 检验法)¶
\(t_0 = \frac{\overline{x} - \mu_0}{s / \sqrt{n}}\) ,当 \(\mu = \mu_0\) 时, \(t = \frac{\overline{X} - \mu_0}{s / \sqrt{n}} \sim t(n-1)\)
(1) \(H_0 : \mu = \mu_0 \leftrightarrow H_1 : \mu \ne \mu_0\)
拒绝域 : \(|t| \ge t_{\alpha / 2}(n-1)\)
P_ = \(P_{\mu_0} \{|t| \ge |t_0| \} = 2P(t(n-1) \ge |t_0|)\)
(2) \(H_0 : \mu \le \mu_0 \leftrightarrow H_1 : \mu > \mu_0\)
拒绝域 : \(t \ge t_{\alpha}(n-1)\)
P_ = \(P_{\mu_0} \{t \ge t_0 \} = P(t(n-1) \ge t_0)\)
(3) \(H_0 : \mu \ge \mu_0 , H_1 : \mu < \mu_0\)
拒绝域 : \(t \le -t_{\alpha}(n-1)\)
P_ = \(P_{\mu_0} \{t \le t_0 \} = P(t(n-1) \le t_0)\)
3 \(\mu\) 未知检验 \(\sigma^2\) (\(\chi^2\) 检验法)¶
当 \(\sigma^2 = \sigma_0^2\) 时, \(\chi^2 = \frac{(n-1)s^2}{\sigma_0^2} \sim \chi^2(n-1)\)
(1) \(H_0 : \sigma^2 = \sigma_0^2 \leftrightarrow H_1 : \sigma^2 \ne \sigma_0^2\)
拒绝域 : \(\chi^2 \le \chi^2_{1-\alpha / 2}(n-1) \text{ 或 } \chi^2 \ge \chi^2_{\alpha / 2}(n-1)\)
(2) \(H_0 : \sigma^2 \le \sigma_0^2 \leftrightarrow H_1 : \sigma^2 > \sigma_0^2\)
拒绝域 : \(\chi^2 \ge \chi^2_{\alpha}(n-1)\)
(3) \(H_0 : \sigma^2 \ge \sigma_0^2 \leftrightarrow H_1 : \sigma^2 < \sigma_0^2\)
拒绝域 : \(\chi^2 \le \chi^2_{1-\alpha}(n-1)\)
P_ 值计算:
设 \(p = P_{\sigma_0^2} \{\frac{(n-1)S^2}{\sigma_0^2} \le \frac{(n-1)s^2}{\sigma_0^2} \} = P\{\chi^2(n-1) \le \chi^2_0 \}\)
其中,对样本观察值 \(x_1, x_2, \cdots, x_n\),\(s^2 = \frac{1}{n-1}\sum\limits_{i=1}^n (x_i - \overline{x})^2\) , \(\chi_0^2 = \frac{(n-1)s^2}{\sigma_0^2}\)
-
对于双边检验
拒绝域 : \(\frac{(n-1)S^2}{\sigma_0^2} \ge \chi^2_{\alpha / 2}(n-1) \text{ 或 } \frac{(n-1)S^2}{\sigma_0^2} \le \chi^2_{1-\alpha / 2}(n-1)\)
P_ = 2min(p,1-p)
当 P_ \(\le \alpha\) , 拒绝原假设,当 P_ \(> \alpha\) , 接受原假设
-
类似的,对于左边检验
\(H_0 : \sigma^2 \ge \sigma_0^2 , H_1 : \sigma^2 < \sigma_0^2\)
拒绝域 : \(\frac{(n-1)S^2}{\sigma_0^2} \le \chi^2_{1-\alpha}(n-1)\)
P_ = p = \(\mathop{sup} P_{H_0} \{\frac{(n-1)S^2}{\sigma_0^2} \le \frac{(n-1)s^2}{\sigma_0^2} \} = P\{\chi^2(n-1) \le \chi^2_0 \}\)
当 P_ \(\le \alpha\) , 拒绝原假设,当 P_ \(> \alpha\) , 接受原假设
-
类似的,对于右边检验
\(H_0 : \sigma^2 \le \sigma_0^2 , H_1 : \sigma^2 > \sigma_0^2\)
拒绝域 : \(\frac{(n-1)S^2}{\sigma_0^2} \ge \chi^2_{\alpha}(n-1)\)
P_ = 1-p = \(\mathop{sup} P_{H_0} \{\frac{(n-1)S^2}{\sigma_0^2} \ge \frac{(n-1)s^2}{\sigma_0^2} \} = P\{\chi^2(n-1) \ge \chi^2_0 \}\)
当 P_ \(\le \alpha\) , 拒绝原假设,当 P_ \(> \alpha\) , 接受原假设
Question
某种元件的寿命 X(以小时记)服从正态分布 \(N(\mu, \sigma^2)\) ,其中 \(\mu\) 和 \(\sigma^2\) 均未知。现测得16只元件的寿命如下:
159 280 101 212 224 379 179 264
222 362 168 250 149 260 485 170
问是否有理由认为元件的平均寿命大于225(小时)?(取显著性水平为0.05)
Answer
按题意需检验
\(H_0 : \mu \le \mu_0 = 225 , H_1 : \mu > \mu_0 = 225\)
拒绝域为 : \(T = \frac{\overline{X} - \mu_0}{S/\sqrt{n}} > t_{\alpha}(n-1)\)
\(n = 16 , t_{0.05}(15) = 1.7531. \overline{x} = 241.5,s = 98.7259\)
计算得 : \(t_0 = \frac{\overline{x} - \mu_0}{s/\sqrt{n}} = 0.6685 < 1.7531\)
没有落在拒绝域内,故不能拒绝原假设,认为元件的平均寿命不大于225小时。
P_ = \(P_{H_0} \{T > t_0 \} = P\{t(15) > 0.6685 \} \approx 0.257 > 0.05\)
因此接受原假设,即认为元件的平均寿命不大于 225 小时。
判断结果与前面一致。
Question
要求某种元件的平均使用寿命不得低于 1000 小时,生产者从一批这种元件中随机抽取 25 件,测得其平均寿命为950小时,标准差为 100 小时。已知这批元件的寿命服从正态分布。试在显著性水平 0.05 下确定这批元件是否合格?
Answer
按题意需检验
\(H_0 : \mu \ge \mu_0 = 1000 , H_1 : \mu < \mu_0 = 1000\)
拒绝域为 : \(t = \frac{\overline{X} - \mu_0}{S/\sqrt{n}} < -t_{\alpha}(n-1)\)
\(n = 25 , t_{0.05}(24) = -1.7109, \overline{x} = 950 , s = 100\)
计算得 : \(t = \frac{\overline{X} - \mu_0}{S/\sqrt{n}} = -2.5 < -1.7109\)
t落在拒绝域内,故拒绝原假设,认为这批元件的平均寿命小于1000小时,不合格。
P_ = \(P_{H_0} \{T < t_0 \} = P\{t(24) < -2.5 \} \approx 0.000866 < 0.05\)
因此拒绝原假设,判断结果与前面一致。
Question
一个园艺科学家正在培养一个新品种的苹果 这种苹果除了口感好和颜色鲜艳以外 另一个重要特征是单个重量差异不大(对照品种的方差 \(\sigma^2 = 7\) ).为了评估新苹果 她随机挑选了 25 个测试重量 (单位:克) 其样本方差为 \(S^2 = 4.25\) 在 \(\alpha = 0.05\) 下检验新品种是否比对照品种方差小?
Answer
\(H_0 : \sigma^2 \ge 7 , H_1 : \sigma^2 < 7\)
查表得 \(\chi^2_{0.95}(24) = 13.848\)
计算得 \(\frac{(25-1)\times 4.25}{7} = 14.57 > 13.848\)
不拒绝原假设,即认为新品种的方差并不比对照组的小。
P_ = \(P\{\chi^2(24) \le 14.57 \} = 0.06729 > 0.05\) 作出同样判断
Question
为了试验两种不同谷物种子的优劣,选取了十块土质不同的土地,并将每块土地分为面积相同的两部分,分别种植这两种种子。设在每块土地的两部分人工管理等条件完全一样。下面给出各块土地上的产量。
| 土地 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 种子A(xi) | 23 | 35 | 29 | 42 | 39 | 29 | 37 | 34 | 35 | 28 |
| 种子B(yi) | 26 | 39 | 35 | 40 | 38 | 24 | 36 | 27 | 41 | 27 |
| di=xi-yi | -3 | -4 | -6 | 2 | 1 | 5 | 1 | 7 | -6 | 1 |
问:以这两种种子种植的谷物产量是否有显著的差异(取显著性水平为0.05)?
Answer
检验假设 \(H_0 : \mu_D = 0 , H_1 : \mu_D \ne 0\)
分别将 \(D_1,D_2,\cdots,D_n\) 的样本均值和样本方差记为 \(\overline{D},S^2_D\)
拒绝域:\(\frac{|\overline{D}|}{S_D/\sqrt{n}} \ge t_{\alpha/2}(n-1)\)
\(n = 10\) 查表得 \(t_{0.025}(9) = 2.2622 ,\\overline{d} = -0.2, s_d = 4.442\)
计算得 \(\frac{|\overline{d}|}{s_d/\sqrt{n}} = 0.142 < 2.2622\)
接受原假设 \(H_0\) 认为两种种子的产量没有显著差异。
两个正态总体参数的假设检验¶
两个正态总体 \(N(\mu_1,\sigma_1^2),N(\mu_2,\sigma_2^2)\) 的检验
\(X_1,X_2,\cdots,X_{n_1}\) 来自 \(N(\mu_1,\sigma_1^2)\) ,\(Y_1,Y_2,\cdots,Y_{n_2}\) 来自 \(N(\mu_2,\sigma_2^2)\)
\(\overline{X} ,\overline{Y},S_1^2,S_2^2\) 分别是 \(X_1,X_2,\cdots,X_{n_1}\) ,\(Y_1,Y_2,\cdots,Y_{n_2}\) 的样本均值和样本方差.显著性水平为 \(\alpha\)
结论¶
1 \(\sigma_1^2,\sigma_2^2\) 已知检验 \(\mu_1-\mu_2\) Z 检验法)¶
当 \(\mu_1 - \mu_2 = \delta\) 时, \(Z = \frac{(\overline{X}-\overline{Y})-\delta}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}} \sim N(0,1)\)
(1) \(H_0 : \mu_1 - \mu_2 = \delta\)
拒绝域 : \(|Z| \ge z_{\alpha/2}\)
(2) \(H_0 : \mu_1 - \mu_2 \le \delta\)
拒绝域 : \(Z \ge z_{\alpha}\)
(3) \(H_0 : \mu_1 - \mu_2 \ge \delta\)
拒绝域 : \(Z \le -z_{\alpha}\)
2 \(\sigma_1^2 = \sigma_2^2\) 未知检验 \(\mu_1-\mu_2\)(t 检验法)¶
当 \(\mu_1 - \mu_2 = \delta\) 时, \(t = \frac{(\overline{X}-\overline{Y})-\delta}{\sqrt{\frac{S_w^2}{n_1}+\frac{S_w^2}{n_2}}} \sim t(n_1+n_2-2)\)
(1) \(H_0 : \mu_1 - \mu_2 = \delta\)
拒绝域 : \(|t| \ge t_{\alpha/2}(n_1+n_2-2)\)
(2) \(H_0 : \mu_1 - \mu_2 \le \delta\)
拒绝域 : \(t \ge t_{\alpha}(n_1+n_2-2)\)
(3) \(H_0 : \mu_1 - \mu_2 \ge \delta\)
拒绝域 : \(t \le -t_{\alpha}(n_1+n_2-2)\)
3 \(\mu_1,\mu_2\) 未知检验 \(\frac{\sigma_1^2}{\sigma_2^2}\)(F 检验法)¶
当 \(\sigma_1^2 = \sigma_2^2\) 时, \(F = \frac{S_1^2}{S_2^2} \sim F(n_1-1,n_2-1)\)
(1) \(H_0 : \sigma_1^2 = \sigma_2^2 \leftrightarrow H_1 : \sigma_1^2 \neq \sigma_2^2\)
拒绝域 : \(F \le F_{1 - \alpha/2}(n_1-1,n_2-1)\) 或 \(F \ge F_{\alpha/2}(n_1-1,n_2-1)\)
(2) \(H_0 : \sigma_1^2 \le \sigma_2^2 \leftrightarrow H_1 : \sigma_1^2 > \sigma_2^2\)
拒绝域 : \(F \ge F_{\alpha}(n_1-1,n_2-1)\)
(3) \(H_0 : \sigma_1^2 \ge \sigma_2^2 \leftrightarrow H_1 : \sigma_1^2 < \sigma_2^2\)
拒绝域 : \(F \le F_{1 - \alpha}(n_1-1,n_2-1)\)
Question
某厂使用两种不同的原料A,B生产同一类型产品。各在一周的产品中取样分析。取用原料A生产的样品 220 件,测得平均重量为 2.46 (公斤),样本标准差 s=0.57(公斤)。取用原料 B 生产的样品 205 件,测得平均重量为 2.55 (公斤),样本标准差为 0.48 (公斤)。设两样本独立,来自两个方差相同的独立正态总体。问在水平 0.05 下能否认为用原料 B 的产品平均重量较用原料 A 的为大。
Answer
检验假设 \(H_0 : \mu_1 \ge \mu_2 , H_1 : \mu_1 < \mu_2\)
拒绝域为 : \(\frac{\overline{X} - \overline{Y}}{\sqrt{\frac{s_w^2}{n_1} + \frac{s_w^2}{n_2}}} < -t_{\alpha}(n_1+n_2-2)\)
\(n_1 = 220, n_2 = 205, \overline{x} = 2.46, \overline{y} = 2.55, s_2 = 0.48\)
\(t_{0.05}(423) \approx z_{0.05} = 1.645,s_w = 0.535,\sqrt{\frac{1}{n_1} + \frac{1}{n_2}} = 0.097\)
计算得 : \(\frac{\overline{X} - \overline{Y}}{\sqrt{\frac{s_w^2}{n_1} + \frac{s_w^2}{n_2}}} = -1.733 < -1.645\)
从而拒绝原假设.
Question
两台机床生产同一个型号的滚珠,从甲机床生产的滚珠中抽取 8 个,从乙机床生产的滚珠中抽取 9 个,测得这些滚珠的直径(毫米)如下:
甲机床 15.0 14.8 15.2 15.4 14.9 15.1 15.2 14.8
乙机床 15.2 15.0 14.8 15.1 14.6 14.8 15.1 14.5 15.0
设两机床生产的滚珠直径分别为 \(X\) , \(Y\) ,且 \(X \sim N(\mu_1,\sigma_1^2),Y \sim N(\mu_2,\sigma_2^2)\)
(1) 检验假设 \(H_0 : \sigma_1^2 = \sigma_2^2 , H_1 : \sigma_1^2 \ne \sigma_2^2 (\alpha = 0.1)\)
(2) 检验假设 \(H_0 : \mu_1 \le \mu_2 , H_1 : \mu_1 > \mu_2 (\alpha = 0.1)\)
(3) 检验假设 \(H_0 : \mu_1 = \mu_2 , H_1 : \mu_1 \ne \mu_2 (\alpha = 0.1)\)
Answer
- 当 \(\mu_1,\mu_2\) 未知时,检验 \(H_0 : \sigma_1^2 = \sigma_2^2 , H_1 : \sigma_1^2 \ne \sigma_2^2\) 的拒绝域为 : \(\frac{S_1^2}{S_2^2} \le F_{1-\alpha/2}(n_1-1,n_2-1)\) 或 \(\frac{S_1^2}{S_2^2} \ge F_{\alpha/2}(n_1-1,n_2-1)\)
查表得 \(F_{0.05}(7,8) = 3.50,F_{0.95}(7,8) = \frac{1}{F_{0.05}(8,7)} = 0.268\)
\(n_1 = 8, n_2 = 9, \overline{x} = 15.05, \overline{y} = 14.9,S_1^2 = 0.0457, S_2^2 = 0.0575\)
计算得 : \(0.268 < \frac{S_1^2}{S_2^2} = 0.795 < 3.50\)
不拒绝原假设,故认为方差没有显著差异。
令 \(p = P(F(7,8) \le 0.795) = 0.3875\)
P_ = 2min(p,1-p) = 0.775 > 0.05 接受原假设
- \(H_0 : \mu_1 \le \mu_2 , H_1 : \mu_1 > \mu_2\)的拒绝域为 : \(\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{S_w^2}{n_1}+\frac{S_w^2}{n_2}}} > t_{\alpha}(n_1+n_2-2)\)
\(t_{0.1}(15) = 1.3406,S_w = 0.228, \sqrt{\frac{1}{n_1}+\frac{1}{n_2}} = 0.486\)
计算得 : \(\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{S_w^2}{n_1}+\frac{S_w^2}{n_2}}} = 1.354 > 1.3406\) 从而拒绝原假设
P_ = \(P\{t(15) \ge 1.354\} = 0.098 < 0.1\)
- \(H_0 : \mu_1 = \mu_2 , H_1 : \mu_1 \ne \mu_2\)的拒绝域为 : \(|\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{S_w^2}{n_1}+\frac{S_w^2}{n_2}}}| \ge t_{\alpha/2}(n_1+n_2-2)\)
计算得 : \(|\frac{\overline{X}-\overline{Y}}{\sqrt{\frac{S_w^2}{n_1}+\frac{S_w^2}{n_2}}}| = 1.354 < t_{0.05}(15) = 1.7531\) 从而接受原假设
P_ = \(2P\{t(15) \ge 1.354\} = 0.196 > 0.1\)
假设检验与区间估计¶
作区间估计时,对参数没有先验的认识,但确定参数是固定不变的,只是未知,所以区间估计的目的是:根据样本对参数进行估计;
作假设检验时,对参数有一个先验的认识(例如 \(\mu=\mu_0\) ),但由于某种情形的出现(如工艺改良等),猜测真实参数值可能发生了变化,所以假设检验的目的是:根据样本确认参数是否真的发生了改变。
但置信区间与假设检验的拒绝域之间又有密切的关系。
考虑单个正态总体方差已知时有关均值的统计推断.
设 \(X_1,X_2,\cdots,X_n\) 是来自总体 \(N(\mu,\sigma^2)\) 的样本,\(\sigma^2\) 已知,\(\mu\) 的置信水平为 \(1-\alpha\) 的置信区间为:
假设检验问题 \(H_0 : \mu = \mu_0 , H_1 : \mu \ne \mu_0\) 显著性水平为 \(\alpha\) 的检验拒绝域为: \(W = \{\frac{|\overline{X}-\mu_0|}{\sigma/\sqrt{n}} \ge z_{\alpha/2}\}\)
接受域为 : \(\overline{W} = \{\frac{|\overline{X}-\mu_0|}{\sigma/\sqrt{n}} < z_{\alpha/2}\} = \{\overline{X} - \frac{\sigma}{\sqrt{n}}z_{\alpha/2} < \mu_0 < \overline{X} + \frac{\sigma}{\sqrt{n}}z_{\alpha/2}\}\)
Note
将接受域中的 \(\mu_0\) 改写成 \(\mu\) 时,所得结果正好是参数 \(\mu\) 的置信水平为 \(1-\alpha\) 的置信区间。
一般地,若检验假设问题 \(H_0 : \theta = \theta_0 , H_1 : \theta \ne \theta_0\) 的显著水平为 \(\alpha\) 的接受域能等价地写成 \(\hat{\theta_L} < \theta_0 < \hat{\theta_U}\) 那么 \((\hat{\theta_L},\hat{\theta_U})\) 就是参数 \(\theta\) 的置信水平为 \(1-\alpha\) 的置信区间。
反之,若 \((\hat{\theta_L},\hat{\theta_U})\) 是 \(\theta\) 的置信水平为 \(1-\alpha\) 的置信区间,则当 \(\theta_0 \in (\hat{\theta_L},\hat{\theta_U})\) 时,接受双边检验 \(H_0 : \theta = \theta_0 , H_1 : \theta \ne \theta_0\) 中的原假设 \(H_0\) ,且检验的拒绝域为 \(\theta_0 \le \hat{\theta_L}\) 或 \(\theta_0 \ge \hat{\theta_U}\) 。
单侧置信限与单边假设检验的关系¶
(1) 若 \(\hat{\theta_L}\) 是 \(\theta\) 的置信水平为 \(1 - \alpha\) 的单侧置信下限,则当 \(\theta_0 \ge \hat{\theta_L}\) 时,接受右边检验 \(H_0 : \theta \le \theta_0 , H_1 : \theta > \theta_0\) 中的原假设 \(H_0\) ,反之,拒绝原假设 \(H_0\) 。
(2) 若 \(\hat{\theta_U}\) 是 \(\theta\) 的置信水平为 \(1 - \alpha\) 的单侧置信上限,则当 \(\theta_0 \le \hat{\theta_U}\) 时,接受左边检验 \(H_0 : \theta \ge \theta_0 , H_1 : \theta < \theta_0\) 中的原假设 \(H_0\) ,反之,拒绝原假设 \(H_0\) 。
拟合优度检验¶
前面介绍的各种检验都是在总体服从正态分布前提下,对参数进行假设检验的。实际中可能遇到这样的情形,总体服从何种理论分布并不知道,要求我们直接对总体分布提出一个假设 。
基本原理和步骤¶
-
在 \(H_0\) 下,将总体 X 取值的全体分成 k 个两两不相交的子集 \(A_1,\dots,A_k\)
-
以 \(n_i(i=1,\dots,k)\) 记样本观察值 \(x_1,\dots,x_n\) 中落在 \(A_i\) 的个数(实际频数).
-
当 \(H_0\) 为真且 \(F_0(x)\) 完全已知时,计算事件 \(A_i\) 发生的概率 \(P_i = P_{F_0}(A_i),i=1,\dots,k\)
当 \(F_0(x)\) 含有 \(r\) 个未知参数时,先利用极大似然法估计 \(r\) 个未知参数,然后求得 \(p_i\) 的估计 \(\hat{p_i}\) ,此时称 \(np_i(\text{或}n\hat{p_i})\) 为理论频数.
- 统计量
反映了实际频数与理论频数的综合偏差,当 \(H_0\) 成立时, \(\chi^2\) 的取值偏小,因此检验的拒绝域形式为 : \(\chi^2 \ge c\)
定理¶
若 \(n\) 充分大,则当 \(H_0\) 为真时,统计量 \(\chi^2\) 近似服从 \(\chi^2(k-r-1)\) 分布,其中 \(k\) 为分类数, \(r\) 为 \(F_0(x)\) 中含有的未知参数个数.
即在显著水平 \(\alpha\) 下拒绝域为
注: \(\chi^2\) 拟合检验使用时必须注意 \(n\) 要足够大, \(np_i(\text{或} n\hat{p_i})\) 不能太小。根据实践,要求 \(n \ge 50\) , \(np_i(\text{或} n\hat{p_i}) \ge 5\) ,否则应适当合并相邻的类以满足要求.
Question
一淘宝店主搜集了一年中每天的订单数 \(X\) ,除去春节期间及双十一前后外,按 330 天计,具体数据如下:
| 订单数 X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 天数 | 3 | 6 | 21 | 46 | 48 | 61 | 52 | 42 |
| 订单数 X | 8 | 9 | 10 | 11 | 12 | 13 | 16 |
|---|---|---|---|---|---|---|---|
| 天数 | 27 | 11 | 6 | 4 | 1 | 1 | 1 |
通常认为每天的订单数服从泊松分布,以上的数据是否支持这个结论?
Answer
\(H_0: X \sim P(\lambda)\) \(\lambda\) 为未知参数, 总订单数为 1749
所以平均每天订单数 \(\hat{\lambda} = \overline{X} = \frac{1749}{330} = 5.3\)
订单数大于 10 的进行合并,对订单数为 \(i(i=0,1,\dots,10,11+)\) 的概率值进行估计:
理论频数 : \(n_i = np_i,i = 0,1,\dots,10,11,n\hat{p_0} = 1.65 < 5\)
将 \(x = 0\) 与 \(x = 1\) 合并,最后共有 11 类,具体结果为
| 订单数 X | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 概率估计 | 0.005 | 0.026 | 0.070 | 0.124 | 0.164 | 0.174 |
| 理论频数 | 1.65 | 8.73 | 23.13 | 40.87 | 54.16 | 57.41 |
| 订单数 X | 6 | 7 | 8 | 9 | 10 | \(\ge\) 11 |
|---|---|---|---|---|---|---|
| 概率估计 | 0.154 | 0.116 | 0.077 | 0.045 | 0.024 | 0.021 |
| 理论频数 | 50.71 | 38.39 | 25.44 | 14.98 | 7.94 | 6.60 |
检验统计量的值为 \(\chi^2 = \sum\limits_{i=1}^{k} \frac{(n_i)^2}{n\hat{p_i}} -n = \sum\limits_{i=1}^{11} \frac{(n_i)^2}{n\hat{p_i}} -330 = 3.97\)
即在显著性水平 \(\alpha = 0.05\) 下临界值 \(chi_{\alpha}^2(k-r-1) = \chi_{0.05}^2(11-1-1) = 16.92\)
于是, \(3.92 < 16.92\) , 不拒绝原假设。
P_ = \(P(\chi^2(9) \ge 3.97) = 0.913\)