HW7(习题三)
约 526 个字 1 张图片 预计阅读时间 3 分钟
A32
Question
设随机变量 \(X,Y\) 相互独立,且分别具有概率分布律
设 \(Z=X+Y\) , \(M = max\{X,Y\}\) , \(N = min\{X,Y\}\) ,分别求 \(Z,M,N\) 的概率分布律.
Answer
1.
| Z |
1 |
2 |
3 |
4 |
5 |
| P |
0.04 |
0.14 |
0.3 |
0.32 |
0.2 |
A38
Question
设随机变量 \(X \sim U(0,1)\) , \(Y\) 的密度函数为
\[f_Y(y)=\begin{cases} 2y & 0 < y < 1 \\ 0 & \text{其他} \end{cases}\]
且 \(X,Y\) 相互独立,记 \(M = max\{X,Y\}, N = min\{X,Y\}\) ,分别求 \(M,N\) 的密度函数.
Answer
1.
\[F_X(x) = \begin{cases} x,&0<x<1 \\ 0,&\text{其他} \end{cases} , F_Y(y) = \begin{cases} y^2,&0<y<1 \\ 0,&\text{其他} \end{cases}\]
\[F_M(t)=t^3,0<t<1,F_N(t) = t+t^2-t^3,0<t<1\]
\[f_M(t)=\begin{cases}3t^2,&0<t<1 \\ 0, &\text{其他}\end{cases},f_N(t)=\begin{cases} 1+2t-3t^2,&0<t<1 \\ 0, &\text{其他} \end{cases}\]
B6
Question
在 \(A\) 地至 \(B\) 地(距离为 \(m\ km\))的公路上,事故发生地在离 \(A\) 地 \(X\ km\) 处, 事故处理车在离 \(A\) 地 \(Y\ km\) 处. 设 \(X\) 与 \(Y\) 均服从 \((0,m)\) 上的均匀分布,且 \(X\) 与 \(Y\) 相互独立,求事故车与事故处理车的距离 \(Z\) 的密度函数.
Answer
1.\(Z = |Y-X|\)由画图得
\[F_Z(t) = \frac{m^2 - (m-t)^2}{m^2} = \frac{2mt - t^2}{m^2},0<t<m\]
\[f_Z(t)=\begin{cases} \frac{2m-2t}{m^2},&0<t<m \\ 0,&\text{其他}\end{cases}\]
B7
Question
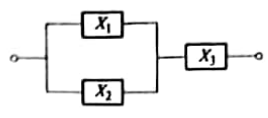
设一系统由三个相互独立的、正常工作时间分别为 \(X_1,X_2,X_3\) 的子系统组成(如图所示),且 \(X_i(i=1,2,3)\) 均服从参数为 \(\lambda\) 的指数分布,求该系统正常工作时间 \(T\) 的分布函数 \(F_T(t)\) 及密度函数 \(f_T(t)\) .
Answer
1.
\[F_{X_1,X_2}(t) = (1-e^{-\lambda t})(1-e^{-\lambda t}) = (1-e^{-\lambda t})^2\]
\[F_T(t) = 1 - [1 - (1-e^{-\lambda t})^2]e^{-\lambda t},t > 0\]
\[f_T(t) = \begin{cases}-3\lambda e^{-3\lambda t} + 4 \lambda e^{-2\lambda t} ,&t > 0 \\ 0,&t \le 0 \end{cases}\]
B10
Question
设二维随机变量 \((X,Y)\) 的联合密度函数为
\[f(x,y)=\begin{cases} \frac{3-x-y}{3}, & 0 < x < 1,0 < y < 2 \\ 0, & \text{其他} \end{cases}\]
记 \(Z = X+Y\) ,求 \(Z\) 的密度函数.
Answer
\[\text{由画图辅助得到}\]
\[f_Z(t) = \int_{-\infty}^{+\infty}f(x,t-x)dx = \begin{cases} \int_0^t \frac{3-t}{3}dx,&0 < t \le 1 \\ \int_0^{1} \frac{3-t}{3}dx,&1 < t \le 2 \\ \int_{t-2}^{1} \frac{3-t}{3}dx,&2 < t \le 3 \\ 0,&\text{其他} \end{cases}\]
\[\therefore f_Z(t) = \begin{cases} \frac{(3-t)t}{3},&0 < t \le 1 \\ \frac{3-t}{3},&1 < t \le 2 \\ \frac{(3-t)^2}{3},&2 < t \le 3 \\ 0,&\text{其他} \end{cases}\]
B11
Question
已知市场上某种蔬菜的价格(单位:元/kg) \(X\sim U(6,8)\) (均匀分布),设某餐馆近期购买该种蔬菜的数量 \(Y\) 为8kg和10kg的概率均为0.5.
(1)求购买金额 \(Z\) 不大于60元的概率 \(p\) ;
(2)求购买金额 \(Z\) 的分布函数 \(F_Z(z)\) .
Answer
1.
\[F_X(x) = \begin{cases} \frac{1}{2}(x-6),& 6<x<8 \\ 0,&\text{其他} \end{cases}\]
\[\therefore P = \frac{1}{2} \times \frac{1}{2} \times (\frac{60}{8}-6) = \frac{3}{8}\]
2.
\[X = \frac{Z}{8}, F_Z(z) = \frac{z}{32} - \frac{3}{2},48<z \le 60\]
\[F_Z(z) = \frac{1}{2} \times \frac{1}{2} \times (\frac{z}{8}-6) + \frac{1}{2} \times \frac{1}{2} \times (\frac{z}{10}-6) = \frac{9z}{160} - 3,60<z \le 64\]
\[F_Z(z) = \frac{1}{2} \times \frac{1}{2} \times (\frac{z}{10}-6) + \frac{1}{2} \times \frac{1}{2} \times (8-6) = \frac{z}{40} - 1,64<z < 80\]
\[\therefore F_Z(z) = \begin{cases} 0,&z<48 \\ \frac{z}{32} - \frac{3}{2},&48<z < 60 \\ \frac{9z}{160} - 3,&60< z \le 64 \\ \frac{z}{40}-1,& 64 < z < 80 \\ 1,&\text{其他} \end{cases}\]
